Dossier

Avete mai osservato due bolle unirsi tra loro? La forma che ne risulta non è casuale, ma risponde ancora una volta al ferreo principio di risparmio cui s’ispira la natura. Come già accade per una singola bolla di sapone, due bolle assumeranno la forma che permette al solido finale di minimizzare la superficie esterna, dato un volume totale pari alla somma dei volumi delle singole bolle.

Ne viene fuori una geometria curiosa, la cosiddetta double bubble, che ancor oggi lascia a bocca aperta fior di matematici. La doppia bolla consiste in due bolle di sapone che si intersecano e sono separate da una sottile membrana avente come bordo proprio l’intersezione delle bolle. È una forma che osserviamo spesso in natura. Tuttavia, se l’evidenza empirica non lascia dubbi sulla forma della doppia bolla, la matematica ha bisogno di certezze, e non è così ovvio dimostrare che il solido che minimizza la superficie sia proprio quello descritto dalla comune osservazione.

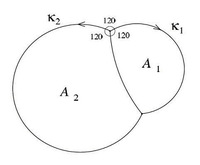
Il problema analogo alla doppia bolla nel piano consiste nell’intersezione di tre archi circolari in due soli punti: nel 1993, il gruppo di ricerca di Alfaro ha dimostrato che l’unica configurazione che racchiude e separa due regioni di piano di area prescritta minimizzando il perimetro è data da tre archi di circonferenza che si incontrano formando tre angoli uguali, ciascuno di 120°. Nel 2002, Morgan ha aggiunto la dimostrazione dell’unicità di questa soluzione: non ci sono quindi altre configurazioni nel piano con la stessa proprietà.

Nello spazio 3D, tuttavia, la situazione è più complessa. L’osservazione suggerisce di ipotizzare che il solido che minimizza la superficie esterna separando due regioni di volume prescritto sia dato da due sfere che si intersecano in una terza porzione di sfera, con angoli di 120°. Dimostrarlo, però, è ben diverso: solo nel 2002, Hutchings dimostrò l’esistenza di questa soluzione, ma non la sua unicità.

Si può dimostrare dunque che la scelta di incontrarsi a 120° sia proprio la più efficiente: ecco perché le celle di un alveare sono a forma di esagono e presentano angoli a 120°! Questa legge fisica è nota come legge di Plateau e descrive in generale la forma assunta da un insieme di bolle nello spazio.

Tuttavia resta aperta la questione dell’unicità; non è ancora stato dimostrato che la forma della doppia bolla standard sia l’unica soluzione geometrica al problema: ci sarà un modo per risparmiare di più?