Quando le bolle diventano tante...
E cosa accade se le bolle sono tante? Quando più di due bolle si uniscono danno vita alle schiume. Anch’esse costituiscono una forte attrazione matematica.
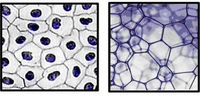 Ma perché tanto interesse? Non è solo pura speculazione. Lo studio delle configurazioni assunte da più bolle di sapone ha delle analogie profonde con lo studio dei tessuti epiteliali (la pelle, le pareti dei vasi sanguigni, le ghiandole del nostro organismo, etc.). Come le bolle, anche le cellule all’interno di un epitelio possono essere descritte come strutture geometriche con un proprio vincolo di volume e soggette ad una tensione superficiale. Insomma, se osserviamo la dinamica di un tessuto nel suo complesso, possiamo affermare che la risposta meccanica di una cellula sia guidata proprio dalle energie superficiali e da un vincolo di volume. La tensione superficiale sembra dunque descrivere molto bene la dinamica di fenomeni quali lo sviluppo embrionale del tessuto epiteliale e l’insorgenza di patologie quali il cancro.
Ma perché tanto interesse? Non è solo pura speculazione. Lo studio delle configurazioni assunte da più bolle di sapone ha delle analogie profonde con lo studio dei tessuti epiteliali (la pelle, le pareti dei vasi sanguigni, le ghiandole del nostro organismo, etc.). Come le bolle, anche le cellule all’interno di un epitelio possono essere descritte come strutture geometriche con un proprio vincolo di volume e soggette ad una tensione superficiale. Insomma, se osserviamo la dinamica di un tessuto nel suo complesso, possiamo affermare che la risposta meccanica di una cellula sia guidata proprio dalle energie superficiali e da un vincolo di volume. La tensione superficiale sembra dunque descrivere molto bene la dinamica di fenomeni quali lo sviluppo embrionale del tessuto epiteliale e l’insorgenza di patologie quali il cancro.
 Di questo si occupa laphysical biology, ramo della ricerca che ha come obiettivo lo studio di sistemi viventi da un punto di vista prettamente fisico matematico, applicando ad essi le leggi che regolano la forma e il comportamento di sistemi non viventi.
Di questo si occupa laphysical biology, ramo della ricerca che ha come obiettivo lo studio di sistemi viventi da un punto di vista prettamente fisico matematico, applicando ad essi le leggi che regolano la forma e il comportamento di sistemi non viventi.
Ecco perché la comunità scientifica ha accolto con entusiasmo gli ultimi studi di due ricercatori statunitensi dell'università della California a Berkeley, Robert Saye e James Sethian, pubblicati su Science nel maggio scorso. Nell’articolo i due ricercatori mostrano una descrizione matematica dell’evoluzione delle schiume, dalla formazione al raggiungimento di una forma stabile. Un nuovo stimolo per comprendere più a fondo la crescita di gruppi di cellule, sfruttando studi matematici che con le cellule sembrano avere ben poco a che spartire. Anche questa, in fondo, è una questione di risparmio!


