Articoli

Un mondo bizzarro

- Scusi, sa che ore sono?

- Sì, lo so.

- Non apra l'ombrello, altrimenti si mette a piovere!

- Poco male, se piove lo chiuderò.

Questa conversazione surreale potrebbe verificarsi in un mondo dove il ragionamento discorsivo segue lo stesso tipo di regole di quello formale. Sarebbe un mondo in cui, se abbiamo l'orologio, risponderemmo solo alla domanda "sa che ore sono?", senza dire l'ora. Oppure sarebbe un mondo in cui se apriamo un ombrello vuol dire che piove, ma se piove ci lasciamo bagnare. O ancora (e questo ci dice che si tratta davvero di un mondo ideale…) chi non mantiene le promesse non può aver vinto le elezioni.

Il lavoro richiesto al cervello nell'elaborare il linguaggio della vita quotidiana è molto più complesso di quello necessario per gli aspetti più elementari della logica. Infatti, quando ci esprimiamo non abbiamo bisogno di esplicitare ogni volta tutte le informazioni necessarie, ci sono fortunatamente dei continui accordi taciti tra i comunicanti. È il cosiddetto Principio Cooperativo, in base al quale quando ci chiedono se sappiamo che ore sono, diamo per scontato che non vorrebbero soffermarsi sul fatto che lo sappiamo o meno, ma sull'ora. Qui il contesto e la memoria giocano un ruolo fondamentale: gran parte delle informazioni necessarie per capirsi rimangono immagazzinate nella memoria o sono implicite nel contesto in cui avviene la conversazione.

Modus tollens e Modus ponens. I sillogismi

Gli altri due esempi di bizzarrie del linguaggio (ombrello ed elezioni) si basano su quella forma di "corretto ragionamento" che va sotto l'espressione latina modus tollens: se p implica q, dalla negazione di q segue anche la negazione di p. Nel linguaggio della logica formale si scrive:

p -%3E q

nonq

CONCLUSIONE: nonp

vale a dire: date le due premesse p -%3E q (p implica q) e nonq (cioè q non è vera), la conclusione logicamente corretta è la negazione di p. Questa del modus tollens è solo una delle tante forme possibili in cui può essere posto un sillogismo: quella costruzione della logica aristotelica in cui da due premesse vere segue necessariamente una conclusione vera. Un altro celebre è il più intuitivo modus ponens, secondo il quale se p implica q ed è vera p, allora segue q. Formalmente:

p -%3E q

p

CONCLUSIONE: q

È importante sottolineare che in entrambi i casi, contrariamente a quanto si tende a pensare con la logica usuale, se p -%3E q e vale qnon si può concludere sempre che vale p, cioè: dalla tesi non segue sempre l'ipotesi. Così come da nonpnon seguenon q, cioè negando l'ipotesi non si nega automaticamente la tesi.

Allora, se p è l'affermazione "non piove" e q è "non apro l'ombrello", il modus tollens ci direbbe che non è vero che se piove (p) apro l'ombrello (q). In compenso però, basta aprire un ombrello (non q) per poter concludere che piove (non p)! Analogamente, se una campagna elettorale si riassume in "se vinco le elezioni (p), allora mantengo le promesse (q)", dovrebbe verificarsi l'utopia che se qualcuno non mantiene le promesse (non q) allora non può aver vinto le elezioni (non p)! Oppure, in base al modus ponens, chi vince mantiene necessariamente le promesse.

Il modus tollens e il modus ponens sono solo due tra le forme più comuni di sillogismo in forma ipotetica. C'è un altro modo di porre i sillogismi: la forma categorica, che è molto più efficiente perché può avvalersi del potentissimo strumento dei diagrammi di Eulero-Venn, che tanto ci aiutano a visualizzare gli insiemi. Ad esempio:

"tutti i francesi sono buongustai"

"qualche buongustaio è ladro"

la conclusione, usando la frettolosa logica comune, sembrerebbe "qualche ladro è francese". In generale, traducendolo nel più astratto linguaggio degli insiemi:

"tutti gli elementi di A sono anche in M" (o per brevità "tutti gli A sono in M")

"qualche M è in B"

CONCLUSIONE: sembrerebbe "qualche B è in A"

A seconda della posizione del termine medio M nelle due premesse, si hanno quattro possibili figure del sillogismo (indicate tradizionalmente con le lettere A, E, I, O). È noto fin dal medioevo che tra tutte le possibili combinazioni di premesse e conclusioni (che per tutte le figure ammontano a 4 x 64 = 256) solo 19 sono corrette, nel senso che la conclusione segue effettivamente dalle premesse. In altri casi invece non si può concludere nulla.

Quest'ultimo caso è proprio quello dell'esempio: la conclusione del sillogismo dei francesi (e, più in generale, quello degli insiemi, qualunque cosa significhino A, B ed M) è che non si può dire nulla. Non è banale senza l'aiuto dei diagrammi che Leonhard Euler inventò per le sue lezioni per corrispondenza (L. Euler, "Lettres a une princesse d'Allemagne" - 1812): la premessa "tutti gli A sono in M" si indica con il diagramma

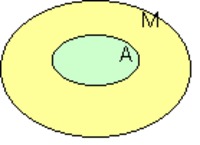
L'altra, "qualche M è in B", può corrispondere equivalentemente ai 5 casi

L'affermazione "qualche M è in B" non dice assolutamente nulla su A, perché a volte B comprende elementi di A, a volte no. L'inghippo sta proprio in questo punto: spesso siamo tentati di invertire implicazioni che non si devono invertire: dal fatto che tutti gli A sono in M, non segue che le informazioni di M si trasferiscono automaticamente anche in A. Ovvero, sapendo che tutti i francesi sono buongustai, non vuol dire che le informazioni sui buongustai si possono attribuire anche ai francesi.

Il significato del quantificatore "qualche" è "almeno uno" (ma eventualmente anche "tutti"). In base alle sole premesse che abbiamo, non possiamo sapere quale dei cinque diagrammi è quello giusto.

I sillogismi nella vita e nella scuola

Ma la logica formale non serve solo a complicare e a rendere bizzarra la vita reale: in molti casi la conoscenza di semplici meccanismi come modus tollens e modus ponens ci eviterebbero ragionamenti assurdi, o di essere sfruttati da pubblicità, mass media, politici, cartomanti, ecc. I pubblicitari, per i quali nessuna parola è messa a caso, si basano proprio su queste piccole "debolezze" del ragionamento umano per concepire i loro slogan: "se bevi questo, allora starai meglio", lasciando intendere che se non lo bevi non starai meglio, o addirittura starai peggio. Invece, se non lo bevi … non succede nulla!

È abbastanza sconcertante (ma anche un po' consolante!) sapere che non sbagliano solo le persone comuni, ma anche chi dovrebbe essere pratico con la ginnastica mentale della logica formale (logici, matematici). È celebre il sillogismo errato con cui Galileo credeva di dare una prova dell'eliocentrismo:

se il sistema è eliocentrico, Venere presenta le fasi

Venere presenta le fasi

il sistema è eliocentrico

La conclusione di Galileo è ovviamente giusta: il sistema planetario è eliocentrico (il sole è in un fuoco dell'orbita), ma essa non segue dal fatto che Venere presenta le fasi.

Secondo Mosconi la discordanza tra pensiero logico e pensiero comune e la non spontaneità del pensiero logico tendono ad attenuarsi quando le risposte al sillogismo sono compatibili con le esigenze della logica comune (G. Mosconi, "Discorso e pensiero", Il Mulino - 1990).

Proprio in queste differenze risiede il valore didattico dei sillogismi: se usati correttamente, dovrebbero educare a ragionare solo in base alle informazioni che si hanno, sfruttandole tutte e senza introdurne altre non richieste. Cosa che gli studenti spesso non riescono a fare. Non è importante allora se nella vita reale la conclusione sarebbe assurda, anzi proprio in quei casi si capisce che la cosa importante per imparare a ragionare è che la conclusione segua dalle premesse, svincolandosi quando si può dai contenuti.

Alcune tra le difficoltà maggiori che studenti e insegnanti, ciascuno dal suo ruolo, incontrano nell'affrontare la matematica stanno nel linguaggio. Allora, sottolineare le differenze tra i due tipi di linguaggio e sapersi spostare da uno all'altro con più agilità migliorerebbe non solo la comprensione della matematica, ma anche l'espressione linguistica, favorendo la lettura e la comprensione di un testo di matematica.

Letture

P. Grice: "Logica e conversazione", Il Mulino - 1993

G. Mosconi: "Discorso e pensiero", Il Mulino - 1990

V. Girotto: "Il ragionamento", Il Mulino - 1994

L. Catastini: "Neuroscienze, apprendimento e didattica della matematica", http://mat.uniroma2.it/mep/Articoli/Art.html - 2001

AA. VV.: "Enciclopedia Garzanti di Filosofia", Garzanti Editore - 1993